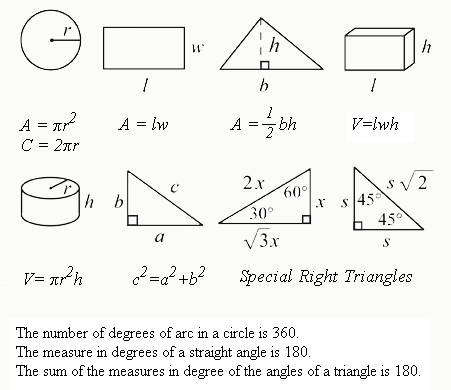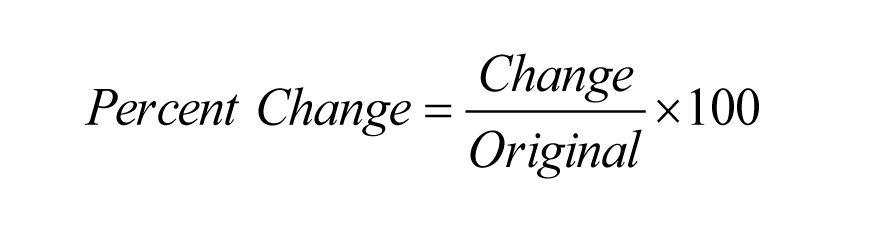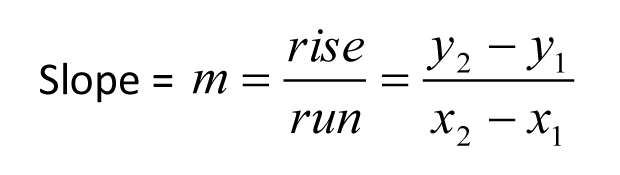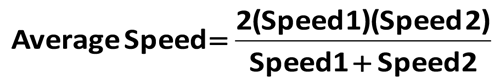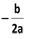The SAT Math Formulas You Should Memorize

(2) The following simple formula will make it very easy for you to solve problems involving Percent Change.

Note that this formula works both for problems involving percent increase and problems involving percent decrease.

Let's look at a simple example:

Suppose that x increases from 8 to 9. By what percent does x increase?

Well, the Original value is 8, and the Change is 9 - 8 = 1. Therefore we have

Percent Change = 1/8 × 100 = 12.5.

So x increases by 12.5%.

(3) To change an average to a sum, use the following.

Sum = Average · Number

This formula can often be used to save a lot of time on statistics questions of all difficulty levels.

Let's look at a simple example.

The average (arithmetic mean) of five numbers is 20. When a sixth number is added, the average of the six numbers is 30. What is the sixth number?

Well, the sum of the five numbers is 20*5 = 100.

The sum of the six numbers is 30*6 = 180.

The sixth number is 180 - 100 = 80.

Here, (x₁,y₁) and (x₂,y₂) are any two points on the line, and m stands for slope. Note that the y-coordinates are subtracted first in the numerator. A common error is to subtract the x-coordinates first. Here is an example.

What is the slope of the line that passes through the two points (-1,3) and (2,5)?

Remark: To get a better understanding of the geometric solution it may be helpful to plot the two points, and visually observe how you would move up, then right to get from the first point to the second point.

(5) In addition to the slope formula, you should know the slope-intercept form of an equation of a line.

y = mx + b

Here, as usual, m is the slope of the line, and b is the y-coordinate of the y-intercept of the line.

In other words, the point (0,b) is on the line. b is where the line hits the y-axis.

As an example, let's write an equation of the line that has a slope of 3 and passes through the point (0,-5).

We are given that m = 3, and b = -5. Thus, the equation of the line in slope-intercept form is

y = 3x - 5.

As a special case of the equation y = mx + b, note that a horizontal line has an equation of the form

y = b

This is because the slope of a horizontal line is 0.

For example, the horizontal line passing through the point (5, 3) has equation y = 3.

You should also know that a vertical line has an equation of the form

x = a

Note that a vertical line has no slope, and therefore cannot be written in slope-intercept form.

For example, the vertical line passing through the point (5, 3) has equation x = 5.

You should also know the following two facts:

Parallel lines have the same slope.

Perpendicular lines have slopes that are negative reciprocals of each other.

(6) The triangle rule states that

the third side of a triangle is between the difference and sum of the other two sides.

This is a very simple rule which is often not taught in the classroom. Triangle rule problems tend to be Level 4 or 5 even though they are usually quite easy. I attribute this to the fact that many students simply have never learned this rule. Here is a simple example.

If x is an integer, how many different triangles are there with sides of length 2, 6 and x?

6 - 2 = 4, and 6 + 2 = 8. By the triangle rule, 4 < x < 8. Since x must be an integer, x can be 5, 6, or 7. So the answer is Three.

(7) This next formula sometimes comes in handy when dealing with sets. If you have a set with X objects and another set with Y objects, then the total number of objects is

Total = X + Y - Both + Neither

Let's look at a simple example.

There are 30 students in a music class. Of these students, 10 play the piano, 15 play the guitar, and 3 play both the piano and the guitar. How many students in the class do not play either of these two instruments?

Substituting these numbers into the formula, we have

30 = 10 + 15 - 3 + N.

So, N = 30 - 22 = 8.

(8) Many students get confused when counting the number of consecutive integers in a list.

The number of integers from a to b, inclusive is b - a + 1.

Remark: The word "inclusive" means that we are including the endpoints a and b.

For example, the number of integers from 2 to 7 is 7 - 2 + 1 = 6.

This can be easily verified with the list 2, 3, 4, 5, 6, 7.

Here is an example that would be harder to verify. 

The number of integers from 62 to 512 is 512 - 62 + 1 =  451 .

(9) One last formula that every student should know.

distance = rate · time

As a simple example, if you drive your car at a speed of 30 miles per hour for 5 hours, then you will travel (30)(5) =  150   miles.  

For many students, that should be sufficient. But for those of you that really want to score an 800, let us look at a few more.

(10) In addition to the simple formula distance = rate · time, the more advanced student might want to memorize the Harmonic Mean Formula.

This formula can be used to find the average speed when 2 individual speeds for the same distance are known. Here is an example.

Dr. Steve drove to work at an average speed of 40 miles per hour, and home from work at an average speed of 60 miles per hour. What was his average speed for the entire round trip, in miles per hour?

We simply plug in the given numbers into the Harmonic Mean Formula. 

Average Speed = 2(40)(60)/(40 + 60) =  48.

Important note: Your intuition might tell you that the answer to this question should be 50 miles per hour. In this case, however, we need to compute the  Harmonic Mean, and  not the  Arithmetic  Mean.

(11) The advanced student may also want to know the Generalized Pythagorean Theorem.

d² = a² + b² + c² 

This simple formula is used to find the length of the long diagonal of a rectangular solid. Here is a straightforward example.

If a box has a length of 3 feet, a width of 4 feet, and height of 12 feet, what is the longest distance from one corner of the box to another corner of the box?

The question is asking for the length of the long diagonal of the box. We just plug the numbers in to the formula for the Generalized Pythagorean Theorem. 

d² = 3² + 4² + 12² = 169. So d = 13.

(12) The general form for a quadratic function is

y = ax² + bx + c.  

The graph of this function is a parabola whose vertex has x-coordinate

The parabola opens upwards if a > 0 and downwards if a < 0.

Here is an example.

Let the function f be defined by f(x) = -2x² - 3x + 2. For what value of x will the function f have its maximum value?

The graph of this function is a downward facing parabola, and we see that a = -2, and b = -3. So the x-coordinate of the vertex is x = 3/(-4) =  -3/4 .

(13) The standard form for a quadratic function is 

y - k = a(x-h)²   

The graph is a parabola with vertex at (h,k). Again, the parabola opens upwards if a > 0 and downwards if a < 0.

Here is an example.

Let the function f be defined by f(x) = 3(x - 1)² + 2. For what value of x will the function f have its minimum value?

The graph of this function is an upward facing parabola with vertex (1,2). Therefore, the answer is 1.

Remark: Note that in this example k = 2, and it is on the right hand side of the equation instead of on the left.

(14) The total number of degrees in the interior of an n-sided polygon is

(n - 2) · 180

Remark: A regular polygon is a polygon with all sides equal in length, and all angles equal in measure.

There are not that many formulas to memorize for SAT math, and many of them you probably already know. So make it a point to commit the rest of these formulas, tested on the SAT math, to memory over the next few days. Then you can focus on practicing SAT math problems.

 
Best of luck,