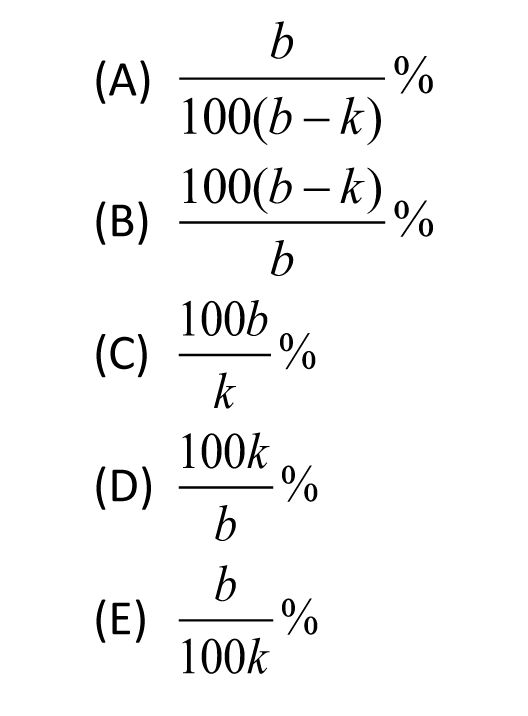Stop Getting Those Last Few Hard SAT Math Questions Wrong

In this article we are going to discuss how to stop getting those last few hard questions wrong. If you are a student currently scoring between a 650 and a 750 in SAT math and you want to get the best possible score, then this is probably one of your main concerns.

Strong math students tend to fall into the trap of doing these last few math questions the same way that they would do them in school. If you are solving a more difficult problem this way, very often you will get tricked. Then, when you look over your answer, the mistake seems "obvious" and you just assume it's a "careless error" (see part 7 of this course for more about "careless errors"). Therefore you don't think about how the problem could have been done differently.

Unfortunately, this will keep happening over and over because those last few problems in the section are unique, and you will never see that particular problem again on an SAT. This is why it is very important to begin to practice solving these problems using SAT specific math strategies .

I want to emphasize that it is not enough to simply know these strategies. You must practice implementing them at the right times. As a very simple example, if question number 20 has variables in the answer choices, DO NOT try to solve this problem using algebra. Use the strategy of picking numbers instead. This particular strategy is very basic and involves substituting in specific numbers for the variables before solving the problem.

As an example, let's look at the following problem.

There are b bricks that need to be stacked. After k of them have been stacked, then in terms of b and k, what percent of the bricks have not yet been stacked?

Since this is a percent problem we choose 100 for the total number of bricks. So b = 100. For k, let's choose 25, so that 25 bricks have been stacked, and 100 - 25 = 75 have not been stacked.

Since we started with 100 as our total, 75% of the bricks have not been stacked. Remember to put a big, dark circle around 75%. We make the substitutions b = 100 and k = 25 into each answer choice.

     (A) 100/7500 ~ 0.0133% (~ means "is approximately")

     (B) 7500/100 = 75%

     (C) 10,000/25 = 400%

     (D) 2500/100 = 25%

     (E) 25/10,000 = 0.0025%

We now compare each of these percents to the percent that we put a nice big, dark circle around. Since (A), (C), (D) and (E) are incorrect we can eliminate them. Therefore the answer is choice (B).

Important note: (B) is not the correct answer simply because it is equal to 75%. It is correct because all 4 of the other choices are not 75%. You absolutely must check all five choices!

For an example of one of my more advanced strategies at work, see this video  where I give a complete solution of another Level 5 SAT math problem.

 
Best of luck,